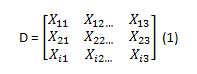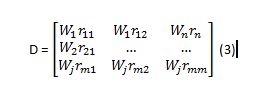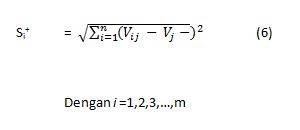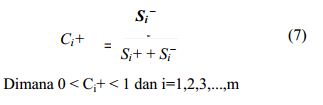Mesran Punya Blog / Mesran [dot]Net Tempat Pemograman

Mesran Punya Blog / Mesran [dot]Net Tempat Pemograman

Apakah kamu tahu apa itu pemograman atau lebih dikenal bahasa Pemograman ? Jangan bingung teman- teman , karna saya akan membawa anda semua yang mau belajar maupun sekilas menambah ilmu pengetahuan,  ke website atau blogspot.com yang penuh dengan bahasa pemograman.

http://mesran.blogspot.com merupakan Website dimana Kita bisa belajar bahasa pemograman dengan berbagai Bahasa Pemograman contohnya (Bahasa C, Bahasa C++, Bahasa C#/C Sharp, Bahasa Pascal, Bahasa Visual(VB 6.0, VB.Net), Bahasa Java, Bahasa Delphi,maupun bahasa pemogramman yang terbaru atau marak – maraknya  yaitu Android).

Tau  caranya ? caranya gampang kok kalau mau mengaksesnya tingal kamu klik nama atau  tulis link  berikut ini http://mesran.blogspot.com atau kamu juga dapat mengunjungi website beliau di  http://mesran.net/ .  Maka anda akan langsung ditujukan ketempat  website yang penuh dengan bahasa pemograman.  Namun, sebelum anda langsung melihat program apa saja yang ada di website tersebut, sebaiknya anda perlu registrasi terlebih dahulu terutama bagi mahasiswa/mahasiswi yang menjadi anak didik beliau dikampus . Agar mudah untuk melihat tugas – tugas yang akan diberikan oleh beliau pada anda, anda cukup membuka link http://mesran.blogspot.com atau http://mesran.net/, maka apa yang anda cari akan tersedia dialamat link tersebut.

Sekian informasi yang bisa saya share kepada teman-teman semua, semoga bermanfaat dan Terima Kasih. Jangan lupa untuk  dikunjungi ya........... :)

Komponen-komponen SPK

SPK terdiri dari 3 (tiga) subsistem utama yang menentukan kapabilitas teknis SPK (Daihani, 2001), yaitu:

1. Sub sistem data (data base)
2. Sub sistem model (model base)
3. Sub sistem dialog (user system interface)

Sub Sistem Data

Subsistem data merupakan komponen SPK penyedia data bagi sistem. Data dimaksud disimpan dalam suatu pangkalan data (data base) yang diorganisasikan oleh suatu sistem yang disebut dengan sistem manajemen pangkalan data (Data Base Management System/DBMS). Melalui manajemen pangkalan data inilah data dapat diambil dan diekstraksi dengan cepat (Daihani, 2001).

Ada beberapa perbedaan antara data base untuk SPK dan non-SPK. Pertama, sumber data untuk SPK lebih “kaya” daripada non-SPK dimana data harus berasal dari luar dan dari dalam karena proses pengambilan keputusan.

Perbedaan lain adalah proses pengambilan dan ektraksi data dari sumber data yang sangat besar. SPK membutuhkan proses ekstraksi dan DBMS yang dalam pengelolaannya harus cukup fleksibel untuk memungkinkan penambahan dan pengurangan secara cepat. Dalam hal ini, kemampuan yang dibutuhkan dari manajemen data base dapat diringkas sebagai berikut (Suryadi dan Ramdhani, 1998):

1. Kemampuan untuk mengkombinasikan berbagai variasi data melalui pengambilan dan ekstraksi data
2. Kemampuan untuk menambahkan sumber data secara tepat dan mudah
3. Kemampuan untuk menggambarkan struktur data logikal sesuai dengan pengertian pemakai sehingga mengetahui apa yang tersedia dan dapat menentukan kebutuhan penambahan dan pengurangan

4. Kemampuan untuk menangani data secara personil sehingga pemakai dapat mencoba berbagai alternatif pertimbangan personil

Kemampuan untuk mengelola berbagai variasi data

Sub Sistem Model

Keunikan dari SPK adalah kemampuannya dalam mengintegrasikan data dengan model-model keputusan. Kalau pada pangkalan data, organisasi data dilakukan oleh manajemen pangkalan data, maka dalam hal ini ada fasilitas tertentu yang berfungsi sebagai pengelola berbagai model yang disebut dengan pangkalan model (model base).

Kendala yang sering kali dihadapi dalam merancang suatu model adalah bahwa model yang disusun ternyata tidak mampu mencerminkan seluruh variabel alam nyata. Sehingga keputusan yang diambil yang didasarkan pada model tersebut menjadi tidak akurat dan tidak sesuai dengan kebutuhan. Oleh karena itu, dalam menyimpan berbagai model pada sistem pangkalan model harus tetap dijaga fleksibilitasnya. Artinya harus ada fasilitas yang mampu membantu pengguna untuk memodifikasi atau menyempurnakan model, seiring dengan perkembangan pengetahuan (Daihani, 2001).

Hal lain yang perlu diperhatikan adalah pada setiap model yang disimpan hendaknya ditambahkan rincian keterangan dan penjelasan yang komprehensif mengenai model yang dibuat, sehingga pengguna atau perancang :

1. Mampu membuat model yang baru dengan mudah dan cepat.
2. Mampu mengakses dan mengintegrasikan subrutin model.
3. Mampu menghubungkan model dengan model yang lain melalui pangkalan data
4. Mampu mengelola model base dengan fungsi manajemen yang analog dengan manajemen data base (seperti mekanisme untuk menyimpan, membuat katalog, menghubungkan dan mengakses model).

Sub Sistem Dialog

Keunikan lainnya dari SPK adalah adanya fasilitas yang mampu mengintegrasikan sistem terpasang dengan pengguna secara interaktif. Fasilitas atau subsistem ini dikenal sebagai subsistem dialog. Melalui sistem dialog inilah sistem diartikulasikan dan diimplementasikan sehingga pengguna atau pemakai dapat berkomunikasi dengan sistem yang dirancang. Fasilitas yang dimiliki oleh subsistem ini dapat dibagi atas tiga komponen (Daihani, 2001), yaitu :

1. Bahasa aksi (action language), yaitu suatu perangkat lunak yang dapat digunakan pengguna untuk berkomunikasi dengan sistem. Komunikasi ini dilakukan melalui berbagai pilihan media sepertikeyboard, joystick, atau key function lainnya.
2. Bahasa tampilan (display atau presentation language), yaitu suatu perangkat yang berfungsi sebagai sarana untuk menampilkan sesuatu. Peralatan yang digunakan untuk merealisasikan tampilan ini diantaranya adalah printer, grafik monitor, plotter, dan lain-lain.
3. Basis pengetahuan (knowledge base), yaitu bagian yang mutlak diketahui oleh pengguna sehingga sistem yang dirancang dapat berfungsi secara efektif.

Kombinasi dari berbagai kemampuan ini dikenal sebagai gaya dialog (dialog style), dimana gaya dialog ini terdiri atas beberapa jenis, diantaranya (Daihani, 2001):

1. Dialog Tanya Jawab, dimana dalam dialog ini sistem bertanya kepada pengguna dan pengguna menjawab, kemudian dari hasil dialog ini sistem akan menawarkan alternatif keputusan yang dianggap memenuhi kebutuhan pengguna
2. Dialog Perintah, dimana dalam dialog ini pengguna memberikan perintah-perintah yang tersedia pada sistem untuk menjalankan fungsi yang ada pada SPK
3. Dialog Menu, dimana model dialog ini merupakan gaya dialog yang paling populer dalam SPK. Dalam hal ini pengguna dihadapkan pada berbagai alternatif menu yang telah disediakan sistem. Menu ini akan ditampilkan pada monitor. Dalam menentukan pilihannya, pengguna sistem cukup menekan tombol-tombol tertentu, dan setiap pilihan akan menghasilkan respon/jawaban tertentu
4. Dialog Masukan/Keluaran, dimana dialog ini menyediakan form input atau masukan. Melalui media ini, pengguna memasukkan perintah dan data. Di samping form input, juga disediakan form keluaran yang merupakan respon dari sistem. Setelah memeriksa keluaran, pengguna dapat mengisi form masukan lainnya untuk melanjutkan dialog berikutnya

Keunikan dari SPK adalah kemampuannya dalam mengintegrasikan data dengan model-model keputusan. Kalau pada pangkalan data, organisasi data dilakukan oleh manajemen pangkalan data, maka dalam hal ini ada fasilitas tertentu yang berfungsi sebagai pengelola berbagai model yang disebut dengan pangkalan model (model base).

Kendala yang sering kali dihadapi dalam merancang suatu model adalah bahwa model yang disusun ternyata tidak mampu mencerminkan seluruh variabel alam nyata. Sehingga keputusan yang diambil yang didasarkan pada model tersebut menjadi tidak akurat dan tidak sesuai dengan kebutuhan. Oleh karena itu, dalam menyimpan berbagai model pada sistem pangkalan model harus tetap dijaga fleksibilitasnya. Artinya harus ada fasilitas yang mampu membantu pengguna untuk memodifikasi atau menyempurnakan model, seiring dengan perkembangan pengetahuan (Daihani, 2001).

Hal lain yang perlu diperhatikan adalah pada setiap model yang disimpan hendaknya ditambahkan rincian keterangan dan penjelasan yang komprehensif mengenai model yang dibuat, sehingga pengguna atau perancang :

1. Mampu membuat model yang baru dengan mudah dan cepat.
2. Mampu mengakses dan mengintegrasikan subrutin model.
3. Mampu menghubungkan model dengan model yang lain melalui pangkalan data
4. Mampu mengelola model base dengan fungsi manajemen yang analog dengan manajemen data base(seperti mekanisme untuk menyimpan, membuat katalog, menghubungkan dan mengakses model).

Metode AHP pada Sistem Penunjang Keputusan (SPK)

 Analytic Hierarchy Process (AHP) merupakan suatu model pendukung keputusan yang  dikembangkan oleh Thomas L. Saaty. Model pendukung keputusan ini  akan menguraikan masalah multi faktor atau multi kriteria yang  kompleks menjadi suatu hirarki. Hirarki  didefinisikan sebagai suatu representasi dari sebuah permasalahan  yang kompleks dalam suatu struktur multi level dimana level pertama  adalah tujuan, yang diikuti level faktor, kriteria, sub kriteria, dan seterusnya ke bawah hingga level terakhir dari alternatif.

AHP membantu para pengambil keputusan untuk memperoleh solusi terbaik dengan mendekomposisi permasalahan kompleks ke dalam bentuk yang lebih sederhana untuk kemudian melakukan sintesis terhadap berbagai faktor yang terlibat dalam permasalahan pengambilan keputusan tersebut. AHP mempertimbangkan aspek kualitatif dan kuantitatif dari suatu keputusan dan mengurangi kompleksitas suatu keputusan dengan membuat perbandingan satu-satu dari berbagai kriteria yang dipilih untuk kemudian mengolah dan memperoleh hasilnya.

AHP sering digunakan sebagai metode pemecahan masalah  dibanding dengan metode yang lain karena alasan-alasan sebagai berikut :

1.    Struktur yang berhirarki, sebagai konsekuesi dari kriteria yang  dipilih, sampai pada subkriteria yang paling dalam.

2.    Memperhitungkan validitas sampai dengan batas toleransi inkonsistensi berbagai kriteria dan alternatif yang dipilih oleh pengambil keputusan.

3.    Memperhitungkan daya tahan output analisis sensitivitas pengambilan keputusan.

Tahapan yang dilakukan dalam metode AHP secara umum digambarkan pada Gambar 1.

 Gambar 1. Tahapan AHP

Tahap 1: Mendefinisikan struktur hirarki masalah

Permasalahan didekomposisi ke dalam bentuk pohon hirarki yang menunjukkan hubungan antara permasalahan, kriteria, dan alternatif solusi.

Tahap 2: Melakukan pembobotan kriteria pada setiap tingkat hirarki

Pada tahapan ini, seluruh kriteria yang berada pada setiap tingkat hirarki diberikan penilaian kepentingan relatif antara satu kriteria dengan kriteria lainnya. Penilaian tersebut menggunakan standar pembobotan Saaty dengan skala berkisar dari 1 hingga 9 dan kebalikannya. Keterangan mengenai skala tersebut dapat dilihat pada tabel 1 berikut:

Tabel 1. Penilaian kepentingan relatif kriteria menggunakan skala Saaty

    

Tahap 3: Menghitung pembobotan kriteria dan konsistensi pembobotan

Tahapan ini menghitung prioritas pembobotan dengan mencari nilai eigenvector dari matriks A.

Konsistensi AHP

Penilaian antara satu kriteria dengan kriteria lain tidak bisa sepenuhnya konsisten. Inkonsistensi ini dapat disebabkan oleh kesalahan memasukkan penilaian ke dalam sistem, kurangnya informasi, kurangnya konsentrasi, dunia nyata yang tidak selalu konsisten, atau model struktur hirarki yang kurang sesuai. Metode AHP mengijinkan terjadinya inkonsistensi penilaian kriteria, tetapi inkonsistensi penilaian tersebut tidak boleh melebihi nilai rasio konsistensi sebesar 10%.

Tabel 2 berikut ini menunjukkan nilai indeks acak untuk setiap matriks berorde 1 hingga 10:

Tabel 2. Nilai indeks acak (RI)

Orde	RI
1	0
2	0
3	0.52
4	0.89
5	1.11
6	1.25
7	1.35
8	1.40
9	1.45
10	1.49

Tahap 4: Menghitung pembobotan alternatif

Pada tahapan ini dilakukan pembobotan alternatif untuk setiap kriteria dalam matriks pairwise comparison. Proses untuk melakukan pembobotan alternatif ini sama dengan proses yang dilakukan untuk menghitung pembobotan kriteria.

Tahap 5: Menampilkan urutan alternatif yang dipertimbangkan dan memilih alternatif

Tahapan ini menghitung nilai eigenvector yang diperoleh pada pembobotan alternatif untuk setiap kriteria dengan nilai eigenvector yang diperoleh pada pembobotan kriteria. Hal ini dilakukan untuk menentukan pilihan dari alternatif yang tersedia. Jumlah nilai terbesar merupakan pilihan yang terbaik.

Metode TOPSIS dalam Sistem Pendukung Keputusan (SPK)

Metode  TOPSIS  adalah  salah  satu  metode  pengambilan  keputusan multikriteria yang pertama kali diperkenalkan oleh Yoon dan Hwang  pada tahun 1981.  Metode  ini  merupakan  salah  satu  metode  yang  banyak  digunakan  untuk menyelesaikan pengambilan  keputusan  secara  praktis.  TOPSIS  memiliki  konsep dimana alternatif  yang terpilih merupakan alternatif terbaik  yang memiliki jarak terpendek dari solusi ideal positif dan jarak terjauh dari solusi ideal negatif [4]. Semakin  banyaknya  faktor  yang  harus  dipertimbangkan  dalam  proses pengambilan  keputusan,  maka  semakin  relatif  sulit  juga  untuk  mengambil
keputusan  terhadap  suatu  permasalahan.  Apalagi  jika  upaya  pengambilan keputusan  dari  suatu  permasalahan  tertentu,  selain  mempertimbangkan  berbagai faktor/kriteria  yang  beragam,  juga  melibatkan  beberapa  orang  pengambil keputusan.  Permasalahan  yang  demikian  dikenal  dengan  permasalahan  multiple criteria decision making  (MCDM).  Dengan kata lain, MCDM juga dapat disebut sebagai  suatu  pengambilan  keputusan  untuk  memilih  alternatif  terbaik  dari sejumlah  alternatif  berdasarkan  beberapa  kriteria  tertentu.  Metode  TOPSISdigunakan  sebagai  suatu  upaya  untuk  menyelesaikan  permasalahan  multiple criteria  decision  making.  Hal  ini  disebabkan  konsepnya  sederhana  dan  mudah dipahami, komputasinya  efisien  dan  memiliki  kemampuan  untuk  mengukur kinerja relatif dari alternatif-alternatif keputusan.

Langkah-langkah Metode TOPSIS

Langkah-langkah yang dilakukan dalam menyelesaikan suatu permasalahan menggunakan metode TOPSIS adalah sebagai berikut [4]:

1. Menggambarkan  alternatif  (m)  dan  kriteria  (n)  ke  dalam  sebuah  matriks, dimana  Xij adalah  pengukuran  pilihan  dari  alternatif  ke-i  dan  kriteria  ke-j.Matriks ini dapat dilihat pada persamaan satu.
    
2. Membuat matriks R yaitu matriks keputusan ternormalisasi Setiap  normalisasi  dari  nilai  rij dapat  dilakukan  dengan  perhitungan menggunakan persamaan dua.
   
3. Membuat pembobotan pada matriks yang telah dinormalisasi Setelah dinormalisasi, setiap kolom pada matriks R dikalikan dengan bobotbobot (wj) untuk menghasilkan matriks pada persamaan tiga.
   
4. Menentukan nilai solusi ideal positif dan solusi ideal negatif. Solusi ideal dinotasikan A+, sedangkan solusi ideal negatif dinotasikan A-. Persamaan untuk menentukan solusi ideal dapat dilihat pada persamaan empat.
   
5. Menghitung separation measure. Separation measure ini merupakan
   pengukuran jarak dari suatu alternatif ke solusi ideal positif dan solusi ideal
   negatif.
   –  Perhitungan solusi ideal positif dapat dilihat pada persamaan lima :
   
   –  Perhitungan solusi ideal negatif dapat dilihat pada persamaan enam :
6. Menghitung  nilai  preferensi  untuk  setiap  alternatif. Untuk  menentukan ranking tiap-tiap alternatif yang ada maka perlu dihitung terlebih dahulu nilai preferensi  dari  tiap  alternatif.  Perhitungan  nilai  preferensi  dapat  dilihat melalui persamaan tujuh.
   Setelah  didapat  nilai  Ci+,  maka  alternatif  dapat  diranking  berdasarkan urutan  Ci+.  Dari  hasil  perankingan  ini  dapat  dilihat  alternatif  terbaik  yaitu alternatif yang memiliki jarak terpendek dari solusi ideal dan berjarak terjauh dari solusi ideal negatif.

Sistem Pendukung Keputusan Menggunakan Metode PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluation)

Deskripsi
Sistem pendukung keputusan adalah suatu sistem berbasis komputer yang ditujukan untuk membantu pengambil keputusan dalam memanfaatkan data dan model tertentu untuk memecahkan berbagai persoalan yang tidak terstruktur. PROMETHEE yang merupakan salah satu metode penentuan urutan atau prioritas dalam analisis multikriteria sangat tepat untuk digunakan karena dugaan dari dominasi kriteria yang digunakan dalam promethee adalah penggunaan nilai dalam hubungan outrangking. Sehingga diperoleh solusi atau hasil dari beberapa alternatif untuk diambil sebuah keputusan. Hasil perangkingan menunjukkan bahwa PROMETHEE I yang berdasarkan pada nilai entering flow dan leaving flow (Perangkingan Parsial) sedangkan PROMETHEE II yang didasarkan pada nilai Net Flow (Perangkingan Lengkap).
Hasil dari penelitian ini adalah sistem pendukung keputusan yang dibangun dengan metode PROMETHEE dapat menentukan urutan alternatif penerima Beasiswa Percikan Iman (BsPI) yang tepat dari berbagai pilihan dengan berbagai kriteria bagi masing-masing alternatif.

Jenis Metode Pengambilan Keputusan Kriteria Majemuk

Ada beberapa metode standar yang umum digunakan untuk pengambilan keputusan Kriteria majemuk adalah Multi Attribute Utility Theory  (MAUT)  (Edward, W, 1997), Simple Multi Attribute Rating Tecnique  (SMART)  (Edward, W dan Barron, FH, 1994), Preference Ranking Organization Method for Enrichment Evaluation  (PROMETHEE) (Brans  et al,  1984)  dan  Analytic Hierarchy Process  (AHP) (Saaty, TL, 1980). Perkembangan ilmu pengambilan keputusan kriteria majemuk juga telah meluas dengan diperkenalkan metode yang lebih kompleks seperti Analytic Network Process (ANP). Penelitian ini mengambil basis metode PROMETHEE sebagai metode untuk memecahkan permasalahan yang dihadapi dalam menentukan kelayakan penerimaan beasiswa.

Metode yang Digunakan dalam SPK

Metode yang digunakan dalam pengambilan keputusan penerima beasiswa ini yaitu menggunakan metode PROMETHEE.

Dasar PROMETHEE

PROMETHEE  adalah salah satu metode penentuan urutan atau prioritas dalam analisis multikriteria atau MCDM (Multi Criterion Decision Making). Dugaan dari dominasi kriteria yang digunakan dalam PROMETHEE  adalah penggunaan nilai dalam  hubungan  outrangking. Masalah pokoknya adalah kesederhanaan, kejelasan dan kestabilan. Semua parameter yang dinyatakan mempunyai pengaruh  nyata menurut pandangan ekonomi.

Data dasar untuk evaluasi dengan methode PROMETHEE disajikan pada Gambar 1 sebagai berikut :

 

                                          Gambar 1 Data Dasar analisis PROMETHEE

Dominasi kriteria 
Nilai f merupakan nilai nyata dari suatu kriteria, f : K → Я (Real Word) dan tujuannya berupa prosedur optimasi untuk setiap  alternatif  yang akan diseleksi,  a ε K,  f(a) merupakan evaluasi dari alternatif yang akan diseleksi tersebut untuk setiap kriteria. Pada saat dua  alternatif  dibandingkan  a,b ε K, harus  dapat ditentukan perbandingan preferensinya.

Penyampaian Intensitas (P) dari preferensi alternatif  a  terhadap alternatif  b sedemikian rupa sehingga:
- P(a,b) = 0,berarti tidak ada beda antara a dan b, atau tidak ada preferensi dari a  lebih baik dari b.
- P(a,b) ≈ 0, berarti lemah preferensi dari a lebih baik dari b.

- P(a,b) = 1, kuat preferensi dari a lebih baik dari b.
- P(a,b) ≈ 1, berarti mutlak preferensi dari a lebih baik dari b.

Dalam metode ini fungsi preferensi seringkali menghasilkan nilai fungsi  yang berbeda antara dua evaluasi, sehingga : P(a,b) = P(f(a)-f(b)).
Untuk semua kriteria, suatu obyek akan dipertimbangkan memiliki nilai kriteria yang lebih baik ditentukan nilai f dan akumulasi dari nilai ini menentukan nilai preferensi atas masing–masing obyek yang akan dipilih.
Setiap kriteria boleh memiliki nilai dominasi  kriteria  atau bobot  kriteria  yang  sama atau berbeda, dan nilai bobot  tersebut harus di atas 0 (Nol). Sebelum menghitung bobot untuk masing-masing kriteria, maka dihitung total bobot dari seluruh kriteria terlebih dahulu. Berikut rumus perhitungan bobot kriteria :

Maka didapat rumus perbandingan untuk setiap alternatif, sebagai berikut :  

 

 

Rekomendasi fungsi preferensi untuk keperluan aplikasi 
Dalam metode  PROMETHEE  ada Enam bentuk fungsi preferensi kriteria. Untuk memberikan gambaran yang lebih baik terhadap area yang tidak sama, maka digunakan tipe fungsi preferensi. Ke Enam tipe preferensi tersebut meliputi : 

 

1.  Tipe Biasa (Usual Criterion) 
Tipe Usual adalah tipe dasar, yang tidak memiliki nilai threshold atau kecenderungan dan tipe ini jarang digunakan. Pada tipe ini dianggap tidak ada beda antara alternatif a dan alternatif b jika a=b atau f(a)=f(b) , maka niliai preferensinya benilai 0 (Nol) atau P(x)=0. Apabila nilai kriteria pada masing-masing alternatif memiliki nilai berbeda, maka  pembuat keputusan membuat  preferensi mutlak  benilai 1 (Satu) atau  P(x)=1 untuk alternatif  yang  memiliki nilai lebih baik. Fungsi  P(x)  untuk preferensi ini disajikan pada gambar 2.

Gambar 2 Tipe Preferensi Usual [7]

2.  Tipe Quasi (Quasi Criterion atau U-Shape) 
Tipe Quasi sering digunakan dalam penilaian suatu data dari segi kwalitas atau mutu, yang mana tipe  ini  menggunakan Satu  threshold  atau  kecenderungan  yang sudah ditentukan,  dalam kasus ini  threshold  itu adalah  indifference.  Indifference ini biasanya dilamabangkan dengan karakter m atau q, dan nilai indifference harus diatas 0 (Nol). Suatu alternatif memiliki  nilai  preferensi yang sama penting selama selisih atau nilai P(x) dari masing-masing alternatif  tidak melebihi nilai  threshold. Apabila selisih hasil evaluasi untuk masing-masing alternatif melebihi nilai  m maka terjadi bentuk preferensi mutlak, jika pembuat memutuskan menggunakan kriteria ini, maka decision maker  tersebut harus menentukan nilai m, dimana nilai ini dapat dijelaskan pengaruh yang signifikan dari sutau kriteria. fungsi P(x) untuk preferensi ini disajikan pada gambar 3.

Gambar 3 Tipe Preferensi Quasi [7]

 

3.  Tipe Linier (Linear Criterion atau V-Shape)
Tipe Linier acapkali digunakan dalam penilaian dari segi kuantitatif atau banyaknya jumlah, yang mana tipe  ini  juga menggunakan Satu  threshold  atau  kecenderungan yang sudah ditentukan,  dalam kasus ini  threshold  itu adalah  preference. Preference ini biasanya  dilamabangkan dengan karakter  n  atau  p, dan nilai  preference  harus diatas 0 (Nol). Kriteria ini menjelaskan bahwa selama nilai selisih memiliki nilai yang lebih rendah dari n, maka nilai preferensi dari pembuat keputusan meningkat secara linier dengan nilai x, jika nilai x lebih besar dibandingkan dengan nilai n, maka terjadi preferensi mutlak. Fungsi P(x) untuk preferensi ini disajikan pada gambar 4.

 Gambar 4 Tipe Preferensi Linear [7]

 

4.  Tipe Tingkatan (Level Criterion) 
Tipe ini mirip dengan  tipe Quasi yang sering digunakan dalam penilaian suatu data dari segi kwalitas atau mutu. Tipe ini  juga menggunakan  threshold indifference (m) tetapi  ditambahkan Satu  threshold  lagi  yaitu  preference  (n). Nilai  indifference serta preference harus diatas 0 (Nol) dan nilai indifference harus di bawah nilai preference. Apabila alternatif tidak memiliki perbedaan (x), maka nilai preferensi sama dengan 0 (Nol)  atau P(x)=0. Jika  x  berada  diatas  nilai m  dan  dibawah nilai  n, hal ini berarti situasi preferensi yang lemah P(x)=0.5. Dan jika x lebih besar atau sama dengan nilai n maka terjadi preferensi mutlak P(x)=1. Fungsi P(x) untuk preferensi ini disajikan pada gambar 5.

Gambar 5 Tipe Preferensi Level [7] 

 

5.  Tipe Linear Quasi (Linear Criterion with Indifference) 
Tipe  Linear Quasi  juga  mirip dengan tipe Linear  yang acapkali digunakan dalam penilaian dari segi  kuantitatif  atau banyaknya jumlah. Tipe ini juga  menggunakan threshold  preference (n) tetapi ditambahkan Satu threshold  lagi yaitu  indifference (m). Nilai indifference  serta  preference  harus diatas 0 (Nol) dan nilai  indifference harus di bawah nilai  preference. Pengambilan keputusan mempertimbangkan peningkatan preferensi secara linier dari tidak berbeda hingga preferensi mutlak dalam  area antara dua kecenderungan  m  dan  n.  Fungsi  P(x)  untuk preferensi ini disajikan pada gambar 6.

 Gambar 6 Tipe Preferensi Linear Quasi [7]

6.  Tipe Gaussian 
Tipe Gaussian sering digunakan untuk mencari nilai aman atau titik aman pada data yang bersifat continue atau berjalan terus.[8] Tipe ini memiliki nilai  threshold yaitu Gaussian  threshold  ( )  yang berhubungan dengan nilai standar deviasi  atau distribusi  normal dalam statistik. fungsi  P(x)  untuk preferensi ini disajikan pada gambar 7.

Gambar 7 Tipe Preferensi Gaussian [7]

 

Nilai threshold atau kecenderungan 
Enam tipe dari  penyamarataan kriteria bisa dipertimbangkan  dalam metode PROMETHEE, tiap-tiap tipe bisa lebih mudah ditentukan  nilai kecenderungannya atau parameternya karena hanya Satu atau Dua parameter yang mesti ditentukan. Hanya tipe Usual saja yang tidak memiliki nilai parameter.

1. Indifference  threshold  yang biasa dilambangkan dalam karakter m atau q.  Jika nilai perbedaan (x) di bawah atau sama dengan nilai  indifference x ≤ m maka x dianggap tidak memiliki nilai perbedaan x = 0.
2. Preference  threshold  yang biasa dilambangkan dalam karakter  n  atau  p. Jika nilai perbedaan (x) di  atas  atau sama dengan nilai  preference  x  ≥  n  maka perbedaan tersebut memiliki nilai mutlak x = 1.
3. Gaussian threshold  yang biasa dilambangkan dalam karakter σ serta diketahui dengan baik sebagai parameter  yang secara langsung berhubungan dengan nilai standar deviasi pada distribusi normal. [5]

Arah dalam grafik nilai outrangking 
Perangkingan yang digunakan dalam metode  PROMETHEE  meliputi tiga bentuk antara lain : 

1.  Entering flow 
Entering flow adalah jumlah dari yang memiliki arah mendekat dari node a dan hal ini merupakan karakter pengukuran outrangking.

Untuk setiap nilai  node  a dalam grafik nilai  outrangking  ditentukan berdasarkan entering flow dengan persamaan :

2.  Leaving flow 
Sedangkan Leaving flow adalah jumlah dari yang memiliki arah menjauh dari node a dan hal ini merupakan pengukuran outrangking. Adapun persamaannya:

3.  Net Flow 
Sehingga pertimbangan dalam penentuan Net flow diperoleh dengan persamaan : 

 

Semakin besar nilai  Entering  flow  dan semakin kecil  Levaing  flow maka alternatif tersebut memiliki kemungkinan dipilih yang semakin besar. Perangkingan dalam PROMETHEE I dilakukan secara parsial,  yaitu didasarkan pada nilai Entering  flow dan Levaing  flow. Sedangkan  PROMETHEE  II termasuk perangkingan komplek karena didasarkan pada nilai Net  flow masing-masing alternatif yaitu alternatif dengan nilai Net flow lebih tinggi menempati satu rangking yang lebih baik.

Langkah-langkah perhitungan dengan metode PROMETHEE 
Langkah-langkah perhitungan dengan metode PROMETHEE adalah sebagai berikut:

1. Menentukan beberapa alternatif
2. Menentukan beberapa kriteria
3. Menentukan dominasi kriteria
4. Menentukan tipe penilaian,  dimana tipe penilaian memiliki 2 tipe yaitu; tipe minimum dan maksimum.
5. Menentukan tipe preferensi untuk setiap kriteria yang paling cocok didasarkan pada data dan pertimbangan  dari  decision maker.  Tipe preferensi ini berjumlah  Enam (Usual, Quasi, Linear, Level, Linear Quasi dan Gaussian).
6. Memberikan nilai  threshold  atau  kecenderungan  untuk setiap kriteria berdasarkan preferensi yang telah dipilih.
7. Perhitungan Entering flow, Leaving flow dan Net flow
8. Hasil pengurutan hasil dari perangkingan

Dalam metode promethee ada 2 macam perangkingan yang disandarkan pada hasil perhitungan, antara lain :

1. Perangkingan parsial yang didasarkan pada nilai Entering flow dan Leaving flow.
2. Perangkingan lengkap atau komplit yang didasarkan pada nilai Net flow.